Exemplo de Regressão no Excel (introdução a Machine Learnig para Predição):

 

Exemplo de Regressão no Excel (introdução a Machine Learnig para Predição): 

     Biomonitor Garcina gardineriana (folhas) para  As na Mata Atlântica

Dados para Importar:

Distan.	As
(m)	(mg/kg)
100	0,98
200	0,95
300	0,85
400	0,86
500	0,59
600	0,45
700	0,32
800	0,15
900	0,11
1000	0,09

 

Coeficiente Linear = 1,1733
É o ponto em que a reta corta o eixo Y, ou o valor do Y (Concentração de As) quando o X é igual a zero (Distancia da Rodovia igual a zero)


Simulação de Distancia da Rodovia e Concentração de Arsênio:
Utilizando a equação da Reta de Regressão estimada: y = -0,0012x + 1,1733.
Quando a Distancia se aproxima de 0 a Concentração de Arsênio se aproxima de 1,1733 mg/Kg.

      Coeficiente Angular ou Coeficiente de Regressão =   -0,0012
Como o Coef. Angular é menor que zero, então a reta é decrescente.
Também podemos dizer que a cada incremento de 1 metro na distancia da rodovia temos um decréscimo de 0,0012 mg/kg de As nas folhas.

     Coeficiente de Determinação ou R Quadrado = 0,9593

Se Coef. Determinação:
0-0,2 = Muito Ruim o Modelo
0,2-0,4 = Ruim
0,4-0,6 = Regular (nem bom nem ruim)
0,6-0,8 = Bom
0,8 - 1 = Muito Bom


O coeficiente de determinação, também chamado de R², é uma medida de ajustamento de um modelo estatístico linear generalizado, como a Regressão linear, em relação aos valores observados. O R² varia entre 0 e 1, indicando, em percentagem, o quanto o modelo consegue explicar os valores observados. Quanto maior o R², mais explicativo é modelo, melhor ele se ajusta à amostra.

Por exemplo, se o R² de um modelo é 0,8234, isto significa que 82,34% da variável dependente  consegue ser explicada pelos regressores presentes no modelo. Fonte Wikipedia.

Saida da Macro do Excel para Regressão

Âmbito cientifico

Resultados e Discussão

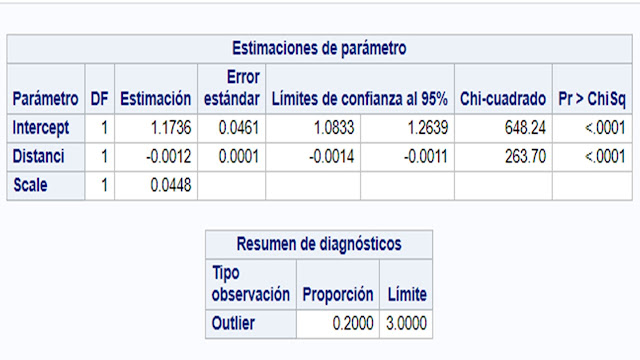
O nível de As nas folhas do biomonitor diminui quando aumenta a distância da Rodovia Anchieta, o coeficiente de regressão, foi -0,00116, altamente significativo ( p < 0,0001), Figura 1.

Âmbito Corporativo

O nível de As nas folhas do biomonitor diminui quando aumenta a distância da Rodovia Anchieta, o coeficiente de regressão, foi -0,00116, com alto nível de confiança (99,999%), Figura 1.

Distan.	As
(m)	(mg/kg)
100	0,98
200	0,95
300	0,85
400	0,86
500	0,59
600	0,45
700	0,32
800	0,15
900	0,11
1000	2,99

Era 0,09

Programa SAS - Regressão Robusta

Data Biomonit;

Input Distanci As;

cards;

100 0.98

200 0.95

300 0.85

400 0.86

500 0.59

600 0.45

700 0.32

800 0.15

900 0.11

1000 2.99

;

Proc print;

Run;

proc robustreg method=m;

  model As = Distanci;

run;

Saida do Programa SAS - Regressão Robusta