Whatsapp Gabriel

 019-988-627-438

Site da Disciplina

 

https://sites.google.com/view/lce136-biologia-esalq-usp

Exercícios

  Exercícios

 

Enviar os exercícios para o e-mail da disciplina.
E-Mail da Disciplina:

biologia.inteligente.10@gmail.com

 

Colocar no Assunto do e-mail o Nome Completo e Número do Exercício

Exercícios:

• Exercício 1 – Crie um exemplo de regressão linear simples, análogo ao de Concentrações de As a Diferentes Distancias da Rodovia Anchieta. Rode no Excel ou Libreoffice Calc e no SAS com Regressão Robusta. Se não conseguir criar o exemplo acompanhe as aulas de resolução de exercícios, quando Gabriel resolverá os exercícios como se fosse um aluno, você terá somente que substituir os sinais de interrogação pelos últimos dígitos de seu RG. Prazo: 9/10/2023

Dados para Importar:

Distan.	As
(m)	(mg/kg)
100	0,98???
200	0,95
300	0,85
400	0,86
500	0,59
600	0,45
700	0,32
800	0,15
900	0,11
1000	0,09

 

• Exercício 2 - Crie um exemplo de regressão múltipla, análogo ao de Biodiversidade Animal. Se não conseguir criar o exemplo acompanhe as aulas de resolução de exercícios, quando Gabriel resolverá os exercícios como se fosse um aluno, você terá somente que substituir os sinais de interrogação pelos últimos dígitos de seu RG. Prazo 16/10/2023

DBO	ICobV	ICArb	Bcont	Dis_Pl	IBD_A
1,604	89	60	11	9	90,???
0,385	90	61	10	8,9	91
0,216	91	62	9	9,1	92
0,303	90	59	10	8,8	89
1,961	20	12	81	0,2	20
0,782	21	14	79	0,3	22
0,57	22	15	78	0,25	23
2,187	22	12	77	0,2	24
0,764	59	35	41	6	60
0,273	60	32	40	6,5	61
1,883	64	33	38	5,8	63
0,581	62	32	37	5,6	62
0,18	79	50	21	8,2	80
0,007	80	49	20	7,8	79
2,028	80	48	18	8,2	81
2,431	79	47	21	7,7	78
1,604	89	60	11	9	90

Arquivo para o SAS

data bda;

input DBO ICobV ICArb Bcont Dis_Pl IBD_A;

cards;

1.604 89 60 11 9 90.???

0.385 90 61 10 8.9 91

0.216 91 62 9 9.1 92

0.303 90 59 10 8.8 89

1.961 20 12 81 0.2 20

0.782 21 14 79 0.3 22

0.57 22 15 78 0.25 23

2.187 22 12 77 0.2 24

0.764 59 35 41 6 60

0.273 60 32 40 6.5 61

1.883 64 33 38 5.8 63

0.581 62 32 37 5.6 62

0.18 79 50 21 8.2 80

0.007 80 49 20 7.8 79

2.028 80 48 18 8.2 81

2.431 79 47 21 7.7 78

1.604 89 60 11 9 11

;

/*

input DBO ICobV ICArb Bcont Dis_Pl IBD_A;

*/

proc robustreg;

model IBD_A = DBO ICobV ICArb 

              Bcont Dis_Pl / diagnostics; 

run;

Arquivo para o Weka

@RELATION biodiv_Animal

@ATTRIBUTE dbo REAL

@ATTRIBUTE  ICob_V REAL

@ATTRIBUTE ICArb REAL

@ATTRIBUTE BCont REAL

@ATTRIBUTE Dist_Pla REAL

@ATTRIBUTE Ibd_A REAL

@DATA

1.604,89,60,11,9,90.???

0.385,90,61,10,8.9,91

0.216,91,62,9,9.1,92

0.303,90,59,10,8.8,89

1.961,20,12,81,0.2,20

0.782,21,14,79,0.3,22

0.57,22,15,78,0.25,23

2.187,22,12,77,0.2,24

0.764,59,35,41,6,60

0.273,60,32,40,6.5,61

1.883,64,33,38,5.8,63

0.581,62,32,37,5.6,62

0.18,79,50,21,8.2,80

0.007,80,49,20,7.8,79

2.028,80,48,18,8.2,81

2.431,79,47,21,7.7,78

• Exercício 3 - Crie um exemplo para rodar cluster analysis, ANOVA e MANOVA. Se não conseguir criar o exemplo acompanhe as aulas de resolução de exercícios, quando Gabriel resolverá os exercícios como se fosse um aluno, você terá somente que substituir os sinais de interrogação pelos últimos dígitos de seu RG Prazo: 23/10/2023.
• Exercício 4 - Crie um exemplo para rodar uma Rede Neural no Weka. Se não conseguir criar o exemplo acompanhe as aulas de resolução de exercícios, quando Gabriel resolverá os exercícios como se fosse um aluno, você terá somente que substituir os sinais de interrogação pelos últimos dígitos de seu RG. Prazo 30/10/2023.

 

 

Aula 25/9/2023

 Pauta:

- Fazermos com toda tranquilidade o Exercicio 1

    - Algum exemplo dos alunos?

    - Fazer o exercicio generico

- Iniciar Exercicio 2

Horario de Consultas e Dados do Gabriel

 Horario de Consultas e Dados do Gabriel

-  Horario de Consultas

       - Sabados das 16 ás 17 horas

        - Link:

                     https://meet.google.com/xgf-jman-pyv

- Whatsapp do Gabriel: 019-988-627-438

- E-Mail do Gabriel: gasarrie@usp.br

Exemplo de Regressão no Excel (introdução a Machine Learnig para Predição):

 

Exemplo de Regressão no Excel (introdução a Machine Learnig para Predição): 

     Biomonitor Garcina gardineriana (folhas) para  As na Mata Atlântica

Dados para Importar:

Distan.	As
(m)	(mg/kg)
100	0,98
200	0,95
300	0,85
400	0,86
500	0,59
600	0,45
700	0,32
800	0,15
900	0,11
1000	0,09

 

Coeficiente Linear = 1,1733
É o ponto em que a reta corta o eixo Y, ou o valor do Y (Concentração de As) quando o X é igual a zero (Distancia da Rodovia igual a zero)


Simulação de Distancia da Rodovia e Concentração de Arsênio:
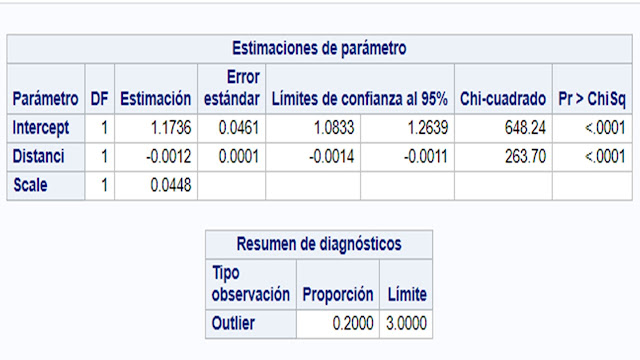
Utilizando a equação da Reta de Regressão estimada: y = -0,0012x + 1,1733.
Quando a Distancia se aproxima de 0 a Concentração de Arsênio se aproxima de 1,1733 mg/Kg.

      Coeficiente Angular ou Coeficiente de Regressão =   -0,0012
Como o Coef. Angular é menor que zero, então a reta é decrescente.
Também podemos dizer que a cada incremento de 1 metro na distancia da rodovia temos um decréscimo de 0,0012 mg/kg de As nas folhas.

     Coeficiente de Determinação ou R Quadrado = 0,9593

Se Coef. Determinação:
0-0,2 = Muito Ruim o Modelo
0,2-0,4 = Ruim
0,4-0,6 = Regular (nem bom nem ruim)
0,6-0,8 = Bom
0,8 - 1 = Muito Bom


O coeficiente de determinação, também chamado de R², é uma medida de ajustamento de um modelo estatístico linear generalizado, como a Regressão linear, em relação aos valores observados. O R² varia entre 0 e 1, indicando, em percentagem, o quanto o modelo consegue explicar os valores observados. Quanto maior o R², mais explicativo é modelo, melhor ele se ajusta à amostra.

Por exemplo, se o R² de um modelo é 0,8234, isto significa que 82,34% da variável dependente  consegue ser explicada pelos regressores presentes no modelo. Fonte Wikipedia.

Saida da Macro do Excel para Regressão

Âmbito cientifico

Resultados e Discussão

O nível de As nas folhas do biomonitor diminui quando aumenta a distância da Rodovia Anchieta, o coeficiente de regressão, foi -0,00116, altamente significativo ( p < 0,0001), Figura 1.

Âmbito Corporativo

O nível de As nas folhas do biomonitor diminui quando aumenta a distância da Rodovia Anchieta, o coeficiente de regressão, foi -0,00116, com alto nível de confiança (99,999%), Figura 1.

Distan.	As
(m)	(mg/kg)
100	0,98
200	0,95
300	0,85
400	0,86
500	0,59
600	0,45
700	0,32
800	0,15
900	0,11
1000	2,99

Era 0,09

Programa SAS - Regressão Robusta

Data Biomonit;

Input Distanci As;

cards;

100 0.98

200 0.95

300 0.85

400 0.86

500 0.59

600 0.45

700 0.32

800 0.15

900 0.11

1000 2.99

;

Proc print;

Run;

proc robustreg method=m;

  model As = Distanci;

run;

Saida do Programa SAS - Regressão Robusta